https://blog.csdn.net/weixin_41190227/article/details/86600821
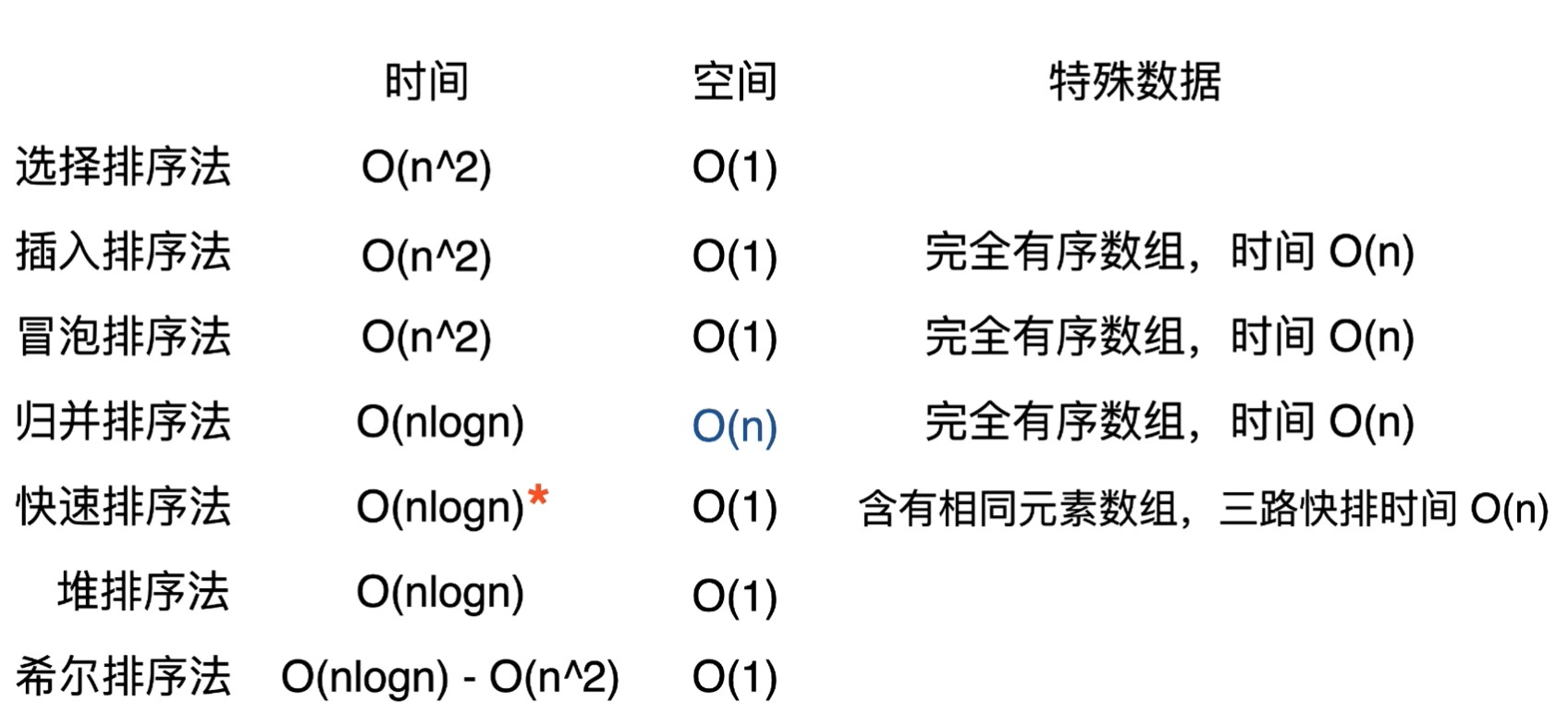
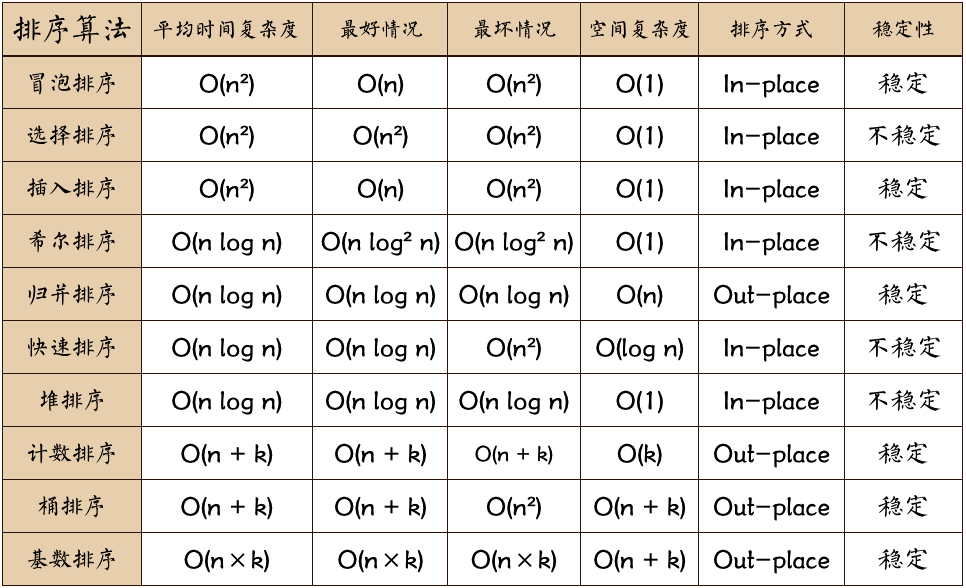
排序算法
选择排序法
- 循环不变量:循环中的每一步
arr[i...n)未排序,arr[0...i)已排序。- 已排序的元素所在位置就是该元素的最终位置。
- 保持:将
arr[i...n)中的最小值与arr[i]位置的值进行交换。
插入排序法
- 循环不变量:循环中的每一步
arr[i...n)未排序,arr[0...i)已排序。- 已排序的元素所在位置是在所有已访问过元素中的相对位置。
- 保持:缓存当前处理的元素,在
arr[0...i)中找到合适的位置,大于它的都向后平移,最后将当前处理元素放在合适的位置。
- 特点:对于有序数组,复杂度为O(n)。适合对近乎有序的数组进行排序,适合对小规模数据排序。
归并排序法
- 递归:对
arr[l,mid]和arr[mid+1,r]这两个区间进行排序,再将两个排序好的子数组进行合并(不能原地合并)。 - 特点:对于有序数组,复杂度为O(n)。
快速排序法
- 递归:选取数组中的随机一个元素作为标定点,将其放到正确的位置上,在它之前的元素都小于它,在它之后的元素都大于它。然后再分别对前半段和后半段进行排序。
- 循环不变量:
arr[l+1...j] < v且arr[j+1...i] >= v。 - 特点:每次划分两个数组的大小近乎相同时性能好。当数组中元素几乎全都相同时会退化为O(n^2)。
- 双路快速排序算法:将小于标定点元素的放在数组左端,将大于标定点元素的放在数组右端。循环不变量为
arr[l+1...i-1]<=v且arr[j+1...r]>=v。可以防止在元素几乎全都相同时退化为O(n^2)。 - 三路快速排序算法:将数组划分为小于、等于、大于三部分。循环不变量为
arr[l+1...lt]<v且arr[gt...r]>v且arr[lt+1...i-1]==v。在元素几乎全都相同时进化为O(n)。
二分查找法
// 左边界下标,有在首元素前的情况可初始化为-1
int l = ?;
// 右边界下标,有在尾元素后的情况可初始化为data.length
int r = ?;
// 在data[l,r]中寻找解
while(l < r){
// 这样写可以防止越界。此时使用语言中默认的向下取整,如果需要向上取整则为l + (r - l + 1)/2
int mid = l + (r - l) / 2;
// 具体逻辑
if(data[mid].compareTo(target) < 0){
……
}
else{
}
}
return l;