牛客网输入输出
- Scanner实例的方法:
- nextInt():直至读取到空格或回车之后结束本次的int值;
- next():直至读取到空格或回车之后结束本次的String值,不可读取回车;
- nextLine():直至读取到换行符(回车)之后结束本次读取的String,可读取回车(空值)。
- 问题:
- nextInt()或者next()读取完毕并回车之后其后紧跟nextLine(),就会导致nextLine()读取到空值,因为nextLine()自动读取到'\n',意味着遇到结束符
- 有时候将字符串转为整数时,代码没问题却提示数组越界,往往是因为字符串代表的整数超过了int的最值,需要改用long。
/*
输入:包括两个正整数a,b(1 <= a, b <= 10^9),输入数据包括多组。
输出:a+b的结果。
*/
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
Scanner in=new Scanner(System.in);
while(in.hasNext()){
int a=in.nextInt();
int b=in.nextInt();
System.out.println(a+b);
}
}
}
/*
输入:第一行包括一个数据组数t(1 <= t <= 100),接下来每行包括两个正整数a,b(1 <= a, b <= 10^9)
输出:a+b的结果
*/
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner in=new Scanner(System.in);
int n=in.nextInt();
while(n-->0){
int a=in.nextInt();
int b=in.nextInt();
System.out.println(a+b);
}
}
}
/*
输入:输入数据有多组, 每行表示一组输入数据。每行不定有n个整数,空格隔开。(1 <= n <= 100)。
输出:每组数据输出求和的结果
*/
import java.util.Scanner;
import java.lang.String;
import java.lang.Integer;
public class Main{
public static void main(String[] args){
Scanner in=new Scanner(System.in);
while(in.hasNext()){
String[] temp=in.nextLine().split(" ");
int sum=0;
for(String s:temp)
sum+=Integer.valueOf(s);
System.out.println(sum);
}
}
}
二分查找法
public <E extends Comparable<E>> int binarySearch(E[] data, E target){
if(data == null || data.length == 0){
return -1;
}
// 左边界下标,有在首元素前的情况可初始化为-1
int left = 0;
// 右边界下标,有在尾元素后的情况可初始化为data.length
int right = data.length-1;
// 在data[l,r]中寻找解
while(left <= right){
// 这样写可以防止越界。此时使用语言中默认的向下取整,如果需要向上取整则为l + (r - l + 1)/2
// int mid = left + ((right - left)>>1);位运算更高效
int mid = left + (right - left) / 2;
// 找到所需元素
if(data[mid].equals(target)){
return mid;
}
// 元素在右半区间
if(data[mid].compareTo(target) < 0){
// 左边界不属于解区间,属于时left = mid
left = mid + 1;
}
// 元素在左半区间
else{
// 右边界不属于解区间,属于时right = mid
right = mid - 1;
}
}
// 没有找到相应元素
return -1;
}
树
前序遍历
public void PreorderTraversal(TreeNode root){
if(root == null){
return;
}
// 使用栈进行遍历
Deque<TreeNode> stack = new ArrayDeque<>();
stack.push(root);
// 先处理当前节点,再处理左子节点,再处理右子节点。
while(!stack.isEmpty()){
TreeNode curnode = stack.pop();
// 在这里可以对当前遍历到的节点进行处理
// ...
// 倒序入栈
if(curnode.right != null){
stack.push(curnode.right);
}
if(curnode.left != null){
stack.push(curnode.left);
}
}
}
中序遍历
public void InorderTraversal(TreeNode root){
if(root == null){
return;
}
// 使用栈进行遍历
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode curnode = root;
// 先处理左子节点,再处理当前节点,再处理右子节点。
while(!stack.isEmpty() || curnode != null){
// 将左子节点压栈
if(curnode != null){
stack.push(curnode);
curnode = curnode.left;
}
// 左子节点全部在栈中,可以开始处理
else{
curnode = stack.pop();
// 在这里可以对当前遍历到的节点进行处理
// ...
curnode = curnode.right;
}
}
}
后序遍历
public void PostorderTraversal(TreeNode root){
if(root == null){
return;
}
// 使用双栈进行遍历,在前序遍历中,先压左再压右可得到一个后序的逆序,再通过另一个栈将序列反转。
Deque<TreeNode> stack1 = new ArrayDeque<>();
Deque<TreeNode> stack2 = new ArrayDeque<>();
stack1.push(root);
while(!stack1.isEmpty()){
TreeNode curnode = stack1.pop();
stack2.push(curnode);
if(curnode.left != null){
stack1.push(curnode.left);
}
if(curnode.right != null){
stack1.push(curnode.right);
}
}
while(!stack2.isEmpt()){
TreeNode curnode = stack2.pop();
// 在这里可以对当前遍历到的节点进行处理
// ...
}
}
层序遍历
public void LevelTraversal(TreeNode root) {
if (root == null){
return;
}
// 使用队列
Deque<TreeNode> queue = new ArrayDeque<>();
queue.add(root);
while (!queue.isEmpty()) {
// 当前层的节点个数
int n = queue.size();
// 遍历当前层的所有节点
for(int i = 0; i < n; i++){
TreeNode curnode = queue.remove();
// 在这里可以对当前遍历到的节点进行处理
// ...
if(curnode.left != null){
queue.add(curnode.left);
}
if(curnode.right != null){
queue.add(curnode.right);
}
}
}
}
线段树
- 线段树是一棵完全二叉树,它的每个结点表示一个区间,主要用于高效解决连续区间的动态查询/区间更新等。
- 懒惰标记:先对修改的数据进行储存,只有在使用的时候才更新线段树。
public interface Merger<E> {
E merge(E a, E b);
}
// 支持的功能:1.构建线段树;2.返回区间[l,r]的值;3.数据源中更新某个值并更新线段树
public class SegmentTree<E> {
// 线段树节点数组
private E[] tree;
// 数据源
private E[] data;
// 含有一个merge方法,实现了已知左右子节点的值求当前节点值的逻辑
private Merger<E> merger;
// 构造函数
public SegmentTree(E[] arr, Merger<E> merger){
this.merger = merger;
data = (E[])new Object[arr.length];
for(int i = 0 ; i < arr.length ; i ++)
data[i] = arr[i];
// 若数据源大小为n,线段树大小为4n(可以设计专用节点,变成链式的动态线段树)
tree = (E[])new Object[4 * arr.length];
buildSegmentTree(0, 0, arr.length - 1);
}
// 在treeIndex的位置创建表示区间[l...r]的线段树
private void buildSegmentTree(int treeIndex, int l, int r){
// 到达叶子节点,进行赋值
if(l == r){
tree[treeIndex] = data[l];
return;
}
// 获取当前节点左右子节点在数组中的下标
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
// 将区间分半,对左半和右半分别建立树
int mid = l + (r - l) / 2;
buildSegmentTree(leftTreeIndex, l, mid);
buildSegmentTree(rightTreeIndex, mid + 1, r);
// 整合左子区间和右子区间,获得当前节点的值
tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
}
// 获取数据个数
public int getSize(){
return data.length;
}
// 获取下标为index的数据
public E get(int index){
if(index < 0 || index >= data.length)
throw new IllegalArgumentException("Index is illegal.");
return data[index];
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子节点的索引
private int leftChild(int index){
return 2*index + 1;
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
private int rightChild(int index){
return 2*index + 2;
}
// 返回区间[queryL, queryR]的值
public E query(int queryL, int queryR){
if(queryL < 0 || queryL >= data.length ||
queryR < 0 || queryR >= data.length || queryL > queryR)
throw new IllegalArgumentException("Index is illegal.");
return query(0, 0, data.length - 1, queryL, queryR);
}
// 在以treeIndex为根的线段树中[l...r]的范围里,搜索区间[queryL...queryR]的值
private E query(int treeIndex, int l, int r, int queryL, int queryR){
// 当前节点表示的区间正是所要查询的区间
if(l == queryL && r == queryR)
return tree[treeIndex];
// treeIndex的节点分为[l...mid]和[mid+1...r]两部分
int mid = l + (r - l) / 2;
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
if(queryL >= mid + 1)
// 查询范围落在右子节点上
return query(rightTreeIndex, mid + 1, r, queryL, queryR);
else if(queryR <= mid)
// 查询范围落在左子节点上
return query(leftTreeIndex, l, mid, queryL, queryR);
// 查询范围在两个子节点上都有,就分别查询再合并
E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
return merger.merge(leftResult, rightResult);
}
// 将index位置的值,更新为e
public void set(int index, E e){
if(index < 0 || index >= data.length)
throw new IllegalArgumentException("Index is illegal");
data[index] = e;
set(0, 0, data.length - 1, index, e);
}
// 在以treeIndex为根的线段树中更新index的值为e
private void set(int treeIndex, int l, int r, int index, E e){
// 到达叶子节点,更新值
if(l == r){
tree[treeIndex] = e;
return;
}
// treeIndex的节点分为[l...mid]和[mid+1...r]两部分
int mid = l + (r - l) / 2;
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
if(index >= mid + 1)
set(rightTreeIndex, mid + 1, r, index, e);
else // index <= mid
set(leftTreeIndex, l, mid, index, e);
// 更新当前节点的值
tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
}
}
并查集
- 是一种特殊的树形结构,每个节点都可以指向它的父节点。用于高效解决连接问题(给出图中任意两点,求两个点是否是相连的,比路径问题回答的内容更少)或者用于求两个集合的并集。主要支持两个动作:
- union(p, q):将两个数据p/q所在的集合进行合并。
- isConnected(p, q):判定p/q是否属于同一个集合。(p/q是ID而不关心元素具体细节)
- 时间复杂度(添加了路径压缩):O(log*n),比O(logn)小
// 适合静态处理元素
public class UnionFind{
// rank[i]表示以i为根的集合所表示的树的层数
// 在后续的代码中, 我们并不会维护rank的语意, 也就是rank的值在路径压缩的过程中, 有可能不在是树的层数值
// 这也是我们的rank不叫height或者depth的原因, 他只是作为比较的一个标准
private int[] rank;
private int[] parent; // parent[i]表示第i个元素所指向的父节点
// 构造函数
public UnionFind(int size){
rank = new int[size];
parent = new int[size];
// 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
for( int i = 0 ; i < size ; i ++ ){
parent[i] = i;
rank[i] = 1;
}
}
public int getSize(){
return parent.length;
}
// 查找过程, 查找元素p所对应的集合编号
// O(h)复杂度, h为树的高度
private int find(int p){
if(p < 0 || p >= parent.length)
throw new IllegalArgumentException("p is out of bound.");
while( p != parent[p] ){
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
// 查看元素p和元素q是否所属一个集合
// O(h)复杂度, h为树的高度
public boolean isConnected( int p , int q ){
return find(p) == find(q);
}
// 合并元素p和元素q所属的集合
// O(h)复杂度, h为树的高度
public void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if( pRoot == qRoot )
return;
// 根据两个元素所在树的rank不同判断合并方向
// 将rank低的集合合并到rank高的集合上
if( rank[pRoot] < rank[qRoot] )
parent[pRoot] = qRoot;
else if( rank[qRoot] < rank[pRoot])
parent[qRoot] = pRoot;
else{ // rank[pRoot] == rank[qRoot]
parent[pRoot] = qRoot;
rank[qRoot] += 1; // 此时, 我维护rank的值
}
}
}
// 树形,适合动态处理元素
private class UnionFind{
// 并查集的rank
int r = 1;
// 指向自己则为根节点,否则为根节点的下层节点
UnionFind parent;
public UnionFind(int rank){
parent = this;
}
private UnionFind find(){
if(parent.parent != parent){
parent = parent.find();
}
return parent;
}
public boolean isConnected(UnionFind another){
return this.find() == another.find();
}
// 合并两个并查集
public void unionElements(UnionFind another){
UnionFind thisroot = this.find();
UnionFind anotherroot = another.find();
if(thisroot == anotherroot)
return;
if(thisroot.r < anotherroot.r)
thisroot.parent = anotherroot.parent;
else if(anotherroot.r < thisroot.r)
anotherroot.parent = thisroot.parent;
else{
thisroot.parent = anotherroot.parent;
anotherroot.r++;
}
}
}
字典树/前缀树
- 是一个专用于处理字符串的多叉树。将单词按字母拆开,每遍历到一个节点都是一个单词,每个节点有26个子节点。查询每个条目的时间复杂度和条目个数无关,而与查询字符串的长度有关。
class Trie {
private class Node{
public boolean isWord;
public Map<Character, Node> next;
public Node(boolean isWord){
this.isWord = isWord;
next = new TreeMap<>();
}
public Node(){
this(false);
}
}
private Node root;
/** Initialize your data structure here. */
public Trie() {
root = new Node();
}
// 向树中插入一个单词
public void insert(String word) {
Node cur = root;
for(int i = 0 ; i < word.length() ; i ++){
char c = word.charAt(i);
if(cur.next.get(c) == null)
cur.next.put(c, new Node());
cur = cur.next.get(c);
}
cur.isWord = true;
}
// 搜索树中是否存在相应的单词
public boolean search(String word) {
Node cur = root;
for(int i = 0 ; i < word.length() ; i ++){
char c = word.charAt(i);
if(cur.next.get(c) == null)
return false;
cur = cur.next.get(c);
}
return cur.isWord;
}
// 搜索是否存在以prefix开头的前缀
public boolean startsWith(String prefix) {
Node cur = root;
for(int i = 0 ; i < prefix.length() ; i ++){
char c = prefix.charAt(i);
if(cur.next.get(c) == null)
return false;
cur = cur.next.get(c);
}
return true;
}
}
图
|
空间 |
建图时间 |
查看两点是否相邻 |
查找点的所有邻边 |
| 邻接矩阵 |
O(V^2) |
O(E) |
O(1) |
O(V) |
| 邻接表(LinkedList) |
O(V+E) |
O(E),如果查重O(E*V) |
O(V) |
O(V) |
| 邻接表(TreeSet) |
O(V+E) |
O(ElogV) |
O(logV) |
O(V) |
深度优先遍历(DFS)
- 在无向图中的应用:
- 求图的连通分量的个数:在调用dfs的循环中计数。
- 求解每一个连通分量具体包含哪些顶点、判断两个顶点是否相连:将visited数组变为int型,不同的连通分量赋不同的值。
- 求一点到另一点的路径:遍历的过程中记录每一次顶点是从哪一个顶点遍历过来的,倒推回去可以得到一个没有特殊性质的任意路径。
- 单源路径问题:在图中确定一个起始点,找到从这个点开始到其他点的路径。
- 所有点对路径问题:定义一个数组,存储每一个顶点对应的单源路径问题的解。
- 检测无向图中的环:求一点到另一点的路径,但起始点和终点是同一个点,在某一点的相邻节点中,找到了一个被访问过的节点,且该节点不是当前节点的上一个节点,就说明找到了一个环。
- 判断图是否是树:图中没有环,图是连通的。
- 判断一个图是否是二分图(顶点V可以分成不相交的两部分;所有的边的两个端点隶属于不同的部分):染色,对一个顶点染成蓝色,它的相邻顶点染成绿色,判断是否所有绿色顶点的相邻顶点都是蓝色顶点,蓝色顶点的相邻顶点都是绿色顶点。

// 在调用dfs时,需要有一个循环,来解决图中有多个连通分量的情况
// 从顶点v开始,进行非递归的深度优先遍历
private void dfs(int v, boolean[] visited){
// 用栈遍历
Stack<Integer> stack = new Stack<>();
// 遍历结果
List<Integer> result = new ArrayList<>();
// 首先将v压入栈,同时,要记录visited[v]为true
stack.push(v);
visited[v] = true;
// 只要栈不为空,说明还有未被遍历的节点
while(!stack.empty()){
// 遍历栈顶元素
int cur = stack.pop();
result.add(cur);
// 由于二叉树只有左右两个孩子,所以分别将他们压入栈就好了
// 但是对于图,和 cur 相邻的顶点可能有多个,需要这个循环
for(int w: G.adj(cur))
// 每次遍历到一个和 cur 相邻的顶点 w,别忘了判断一下 w 是否已经被访问过了
if(!visited[w]){
// 如果 w 没有被访问过,将 w 压入栈中,等待后续遍历
stack.push(w);
// 不要忘记维护visited,让visited[w] = true
visited[w] = true;
}
}
}
广度优先遍历(BFS)
- 作为图的一种遍历方式,BFS也可以实现求解联通分量问题、环检测问题、二分图检测问题等。
- 特殊性质:
- 单源最短路径:使用BFS求解单源路径问题,得到的结果是最短路径(之一)。后遍历到的点距离起始点更远。
- 在遍历中记录dis信息,可以记录到起始点的距离,可以求出无权图的最短路径。
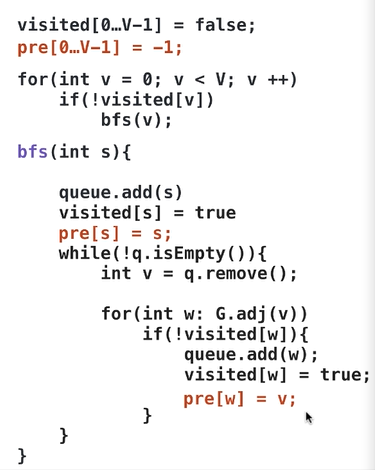
有权图的最短路径
Dijkstra算法
Bellman-Ford算法
Floyd算法
栈和队列
单调栈
- 栈里面存放的数据都是有序的。用于求解以
A[i]为最大值(递增栈)或最小值(递减栈)的数组中左右最大子区间。
// 面试题 17.21. 直方图的水量
public int trap(int[] height) {
int res = 0;
// 单调递增栈,栈顶到栈底单调递增,记录以height[i]为最小值向左右延伸的区间。
Deque<Integer> stack = new ArrayDeque<>();
// 当前遍历到第i个元素
for(int i = 0; i < height.length; i++){
// 栈不为空,且新元素比栈顶元素大,弹出栈顶元素直到栈顶元素大于新元素
while(!stack.isEmpty() && height[i] >= height[stack.peekLast()]){
// 当前最小值
int minHeight = height[stack.pollLast()];
if(stack.isEmpty()){
break;
}
int maxHeight = Math.min(height[i], height[stack.peekLast()]);
res += (maxHeight - minHeight) * (i - stack.peekLast() - 1);
}
// 栈为空或新元素比栈顶元素小,只需要加入到栈中
stack.offerLast(i);
}
return res;
}
动态规划
- 只要涉及求最值,一定是穷举所有可能的结果,然后对比得出最值。穷举主要有两种算法,就是回溯算法和动态规划,前者就是暴力穷举,而后者是根据状态转移方程推导状态。
- 动态规划问题具有以下三个特点:
- 最优子结构:如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构。
- 无后效性:即某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与当前状态有关。
- 重复子问题:即子问题之间是不独立的,一个子问题在下一阶段决策中可能被多次使用到。(该性质并不是动态规划适用的必要条件,但是如果没有这条性质,动态规划算法同其他算法相比就不具备优势)
线性动态规划
- 特点:状态的推导是按照问题规模 i 从小到大依次推过去的,较大规模的问题的解依赖较小规模的问题的解。
- 状态定义:
dp[n] := [0..n]上问题的解
- 状态转移:
dp[n] = f(dp[n-1], ..., dp[0])
- 应用:单串、双串、矩阵等问题规模可以完全由位置表示的场景。
- 依赖比i小的O(1)个子问题。
- 依赖比i小的O(n)个子问题。
最长上升子序列(LIS)
public int lengthOfLIS(int[] nums) {
int len = nums.length;
if (len < 2) {
return len;
}
//dp[i]表示以nums[i]结尾的上升子序列的长度
int[] dp = new int[len];
// dp[i] = 1,第i个字符显然是长度为1的上升子序列
Arrays.fill(dp, 1);
// 当前考虑元素为nums[i]
for (int i = 1; i < len; i++) {
// nums[j]为位于nums[i]之前的元素
for (int j = 0; j < i; j++) {
// nums[i] 可以接在nums[j]子序列之后
if (nums[j] < nums[i]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
// 找到dp[i]的最大值
int res = 0;
for (int i = 0; i < len; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
最大子序列和
// Kadane算法:在数组或滑动窗口中找到子串和的最大值或最小值的 O(N) 算法
public int maxSubArray(int[] nums) {
// dp[i]表示以第i个数结尾的连续子数组最大和
// 滚动数组:dp[i] = Math.max(dp[i - 1] + nums[i], nums[i])因此只需一个空间保存dp[i-1]
int dp = 0;
int maxAns = nums[0];
for (int num : nums) {
dp = Math.max(dp + num, num);
maxAns = Math.max(maxAns, dp);
}
return maxAns;
}
打家劫舍
public int rob(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int length = nums.length;
if (length == 1) {
return nums[0];
}
// dp[i] 表示前i间房屋能偷窃到的最高总金额,使用滚动数组思想缩减为两个空间
// first为dp[i-2],second为dp[i-1]
int first = nums[0], second = Math.max(nums[0], nums[1]);
for (int i = 2; i < length; i++) {
// dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
int tmp = second;
second = Math.max(first + nums[i], second);
first = tmp;
}
return second;
}
最长的斐波那契子序列的长度
// 将斐波那契式的子序列中的两个连续项A[i], A[j]视为单个结点(i, j),整个子序列是这些连续结点之间的路径
public int lenLongestFibSubseq(int[] A) {
int N = A.length;
// 根据数组的值找到数组的下标
Map<Integer, Integer> index = new HashMap<>();
for (int i = 0; i < N; ++i)
index.put(A[i], i);
// 设 longest[i, j] 是结束在 [i, j] 的最长路径
Map<Integer, Integer> longest = new HashMap<>();
int ans = 0;
// 当前遍历到下标为k的元素
for (int k = 0; k < N; ++k)
// 维护longest[j, k]
for (int j = 0; j < k; ++j) {
// i 由 A.index(A[k] - A[j]) 唯一确定,如果数组中没有该元素则返回-1
int i = index.getOrDefault(A[k] - A[j], -1);
// 找到了这样的i,则longest[j, k] = longest[i, j] + 1
if (i >= 0 && i < j) {
// Encoding tuple (i, j) as integer (i * N + j)
int cand = longest.getOrDefault(i * N + j, 2) + 1;
longest.put(j * N + k, cand);
ans = Math.max(ans, cand);
}
}
return ans >= 3 ? ans : 0;
}
最大平均值和的分组
public double largestSumOfAverages(int[] A, int K) {
int N = A.length;
// 前缀和:P[i+1]表示从A[0]到A[i]的和
// 平均值AVE[j+1, i] = (P[i + 1] - P[j + 1] / (i - j))
double[] P = new double[N+1];
for (int i = 0; i < N; ++i)
P[i+1] = P[i] + A[i];
//
// dp[i][k]为将A[i:]切分k次得到的最大数,计算当前k只需要k-1的数据
double[] dp = new double[N];
// 初始化,不分段
for (int i = 0; i < N; ++i)
dp[i] = (P[N] - P[i]) / (N - i);
// 固定当前分段次数k
for (int k = 1; k < K; ++k)
// i为当前起始元素
for (int i = 0; i < N; ++i)
// j>i,将A[i:]分成A[i,j],A[j:]两段
for (int j = i+1; j < N; ++j)
// 如果在j分割,则当前值为后者
dp[i] = Math.max(dp[i], (P[j]-P[i]) / (j-i) + dp[j]);
return dp[0];
}
鸡蛋掉落
// 键为状态[K,N],值为在状态[K,N]的情况下最少需要的步数
Map<Integer, Integer> memo = new HashMap<>();
public int superEggDrop(int K, int N) {
return dp(K, N);
}
// 查找memo[K,N]
public int dp(int K, int N) {
if (!memo.containsKey(N * 100 + K)) {
int ans;
if (N == 0) {
ans = 0;
} else if (K == 1) {
ans = N;
// 二分搜索法
} else {
int lo = 1, hi = N;
while (lo + 1 < hi) {
// 当前搜索值
int x = (lo + hi) / 2;
// dp(K, N)是一个关于N单调递增的函数。
// 鸡蛋摔碎了,dp(K-1, X-1)是一个随X的增加而单调递增的函数
int t1 = dp(K-1, x-1);
// 鸡蛋没摔碎,dp(K,N−X)是一个随X的增加而单调递减的函数。
int t2 = dp(K, N-x);
// 想要使t1,t2的中的最大值最小,就要求它们的交点(离交点最近的点)
// t1<t2时两者的交点大于lo
if (t1 < t2) {
lo = x;
// t1>t2时两者的交点小于lo
} else if (t1 > t2) {
hi = x;
// t1和t2的交点
} else {
lo = hi = x;
}
}
// 需要使t1,t2中的最大值最小
ans = 1 + Math.min(Math.max(dp(K - 1, lo - 1), dp(K, N - lo)), Math.max(dp(K - 1, hi - 1), dp(K, N - hi)));
}
memo.put(N * 100 + K, ans);
}
return memo.get(N * 100 + K);
}
最长公共子序列(LCS)
public int longestCommonSubsequence(String text1, String text2) {
// dp[i][j]表示第一串考虑到第i个字符,第二串考虑到第j个字符时原问题的解
int len1 = text1.length();
int len2 = text2.length();
int[][] dp = new int[len1+1][len2+1];
for(int i = 0; i < len1; i++){
for(int j = 0; j < len2; j++){
if(text1.charAt(i) == text2.charAt(j)){
dp[i+1][j+1] = dp[i][j] + 1;
}
else{
dp[i+1][j+1] = Math.max(dp[i+1][j], dp[i][j+1]);
}
}
}
return dp[len1][len2];
}
最小路径和
public int minPathSum(int[][] grid) {
for (int i = 1; i < grid.length; i++){
grid[i][0] += grid[i - 1][0];
}
for (int j = 1; j < grid[0].length; j++){
grid[0][j] += grid[0][j - 1];
}
for (int i = 1; i < grid.length; i++) {
for (int j = 1; j < grid[i].length; j++) {
grid[i][j] = Math.min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j];
}
}
return grid[grid.length - 1][grid[0].length - 1];
}
前缀和
- 对于给定的序列
num[n],创建sum[n+1],其中sum[0] = 0,sum[i] = sum[i-1] + num[i-1],则有[0,i]上的和为sum[i+1],[i,j]上的和为sum[j+1] - sum[i]。
- 若条件为
[i,j]子序列和为k,则sum[j+1] - sum[i] == k,即sum[i] == sum[j+1] - k,若当前遍历到j+1,可以获得满足条件的i值。
- 可以使用哈希表(集合/映射)、线段树等数据结构维护前缀和。
- 键是前缀和(状态)的值,值为第一次出现时的索引。
- 键是前缀和(前缀状态)的值,值为出现次数。
- 键是前缀和模 K 的余数(可以理解为前缀状态,状态为前缀和模 K)
- 在有些问题中,计算答案时同时需要用到前缀和和后缀和
- 推广:如果想将某种运算应用到前缀元素上,并且利用前缀的结果快速计算区间结果,需要该运算满足区间减法:区间
A = [i, j],区间B = [i, k]区间C = [k+1, j],那么有了大区间A上的结果a和其中一个小区间B上的结果b, 要能够算出另一个小区间C上的结果c。(异或、乘法等)
- 差分:

元素和为目标值的子矩阵数量
// 对于每一行计算前缀和,对于每一列计算行累加和
public int numSubmatrixSumTarget(int[][] matrix, int target) {
int count = 0;
int rows = matrix.length;
int cols = matrix[0].length;
int[][] sum = new int[rows][cols];
// 计算每一行的前缀和
for(int i = 0; i < rows; i++){
sum[i][0] = matrix[i][0];
for(int j = 1; j < cols; j++)
{
sum[i][j] = sum[i][j-1] + matrix[i][j];
}
}
for(int i = 0; i < cols; i++){
for(int j = i; j < cols;j++){
// 对于给定的[i,j]列范围内,[0,k]范围内,键为子矩阵和,值为子矩阵个数。
Map<Integer, Integer> map = new HashMap<>();
// [0,i]为左上角,[rows-1, j]为右下角的矩阵和
int temp=0;
// 滑动窗口寻找目标值
for(int k = 0; k < rows; k++){
temp += (sum[k][j] - sum[k][i] + matrix[k][i]);
// 此矩阵值为target,增加count
if(temp == target){
count++;
}
if(map.get(temp - target) != null){
count += map.get(temp - target);
}
int value = map.getOrDefault(temp, 0) + 1;
map.put(temp, value);
}
}
}
return count;
}
区间加法
public int[] getModifiedArray(int length, int[][] updates) {
int[] diff = new int[length + 1];
for(int[] update: updates){
diff[update[0]] += update[2];
diff[update[1] + 1] -= update[2];
}
for(int i = 1; i < length; i++){
diff[i] += diff[i-1];
}
return Arrays.copyOf(diff, length);
}
区间动态规划
- 概念:状态的定义和转移都与区间有关,其中区间用两个端点表示。
- 状态定义
dp[i][j] = [i..j]上原问题的解。i变大,j变小都可以得到更小规模的子问题。推导状态一般是按照区间长度从短到长推的。
- 拿到一个单串的问题时,往往不能快速地判断到底是用线性动态规划还是区间动态规划。
- 状态转移:
dp[i][j]仅与常数个更小规模子问题有关:
dp[i][j] = f(dp[i + 1][j], dp[i][j - 1], dp[i + 1][j - 1])
dp[i][j]与O(n)个更小规模子问题有关:一般是枚举[i,j]的分割点,将区间分为[i,k]和[k+1,j],对每个k分别求解(下面公式的f),再汇总(下面公式的g)。
dp[i][j] = g(f(dp[i][k], dp[k + 1][j])) 其中k = i .. j-1
预测赢家
class Solution {
public boolean PredictTheWinner(int[] nums) {
int len = nums.length;
// dp[i][j]表示作为先手,在区间[i,j]里进行选择可以获得的净胜分
/*
净胜分:
甲先手面对区间[i...j]时,
如果甲拿nums[i],那么变成乙先手面对区间[i+1...j],这段区间内乙对甲的净胜分为dp[i+1][j];那么甲对乙的净胜分就应该是nums[i] - dp[i+1][j]。
如果甲拿nums[j],同理可得甲对乙的净胜分为是nums[j] - dp[i][j-1]
*/
// 状态转移方程:dp[i][j] = Math.max(nums[i] - dp[i + 1][j], nums[j] - dp[i][j - 1])
int[][] dp = new int[len][len];
// 初始化
for (int i = 0; i < len; i++) {
dp[i][i] = nums[i];
}
for (int i = len - 2; i >= 0; i--) {
for (int j = i + 1; j < len; j++) {
dp[i][j] = Math.max(nums[i] - dp[i + 1][j], nums[j] - dp[i][j - 1]);
}
}
return dp[0][len - 1] >= 0;
}
}
最长回文子序列
// 注意遍历顺序:i从最后一个字符开始往前遍历,j从i+1开始往后遍历,这样可以保证每个子问题都已经算好了。
public int longestPalindromeSubseq(String s) {
int len = s.length();
// dp[i][j]表示[i,j]区间内最长回文子序列的长度
int[][] dp = new int[len][len];
// 用i遍历当前起始元素下标
for(int i = len - 1; i >= 0; i--){
dp[i][i] = 1;
// 用j遍历当前结束元素下标
for(int j = i + 1; j < len; j++){
// if(j - i == 1){
// dp[i][j] = s.charAt(i) == s.charAt(j) ? 2 : 1;
// }
if(s.charAt(i) == s.charAt(j)){
dp[i][j] = dp[i + 1][j - 1] + 2;
}
else{
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][len-1];
}
奇怪的打印机
public int strangePrinter(String s) {
int len = s.length();
if(len == 0){
return 0;
}
// dp[i][j]表示打印出[i,j]上的字符需要的最少次数
// 1. i单独打一次:dp[i][j] = 1 + dp[i + 1][j]
// 2. i与切分点k一起打(i < k <= j && s[i] == s[k]):dp[i][j] = dp[i+1][k] + dp[k+1][j]
int[][] dp = new int[len][len];
dp[len - 1][len - 1] = 1;
// 用i遍历起始下标
for(int i = len - 2; i >= 0; i--){
// 用j遍历结束下标
for(int j = i; j < len; j++){
if(j > i && s.charAt(i) == s.charAt(j)){
dp[i][j] = dp[i + 1][j];
}
else{
dp[i][j] = 1 + dp[i + 1][j];
}
// 用k遍历切分点
for(int k = i + 1; k < j; k++){
if(s.charAt(i) == s.charAt(k)){
dp[i][j] = Math.min(dp[i][j], dp[i + 1][k] + dp[k + 1][j]);
}
}
}
}
return dp[0][len - 1];
}
布尔运算
class Solution {
// 1&1=1/1&0=0/0&1=0/0&0=0
// 1|1=1/1|0=1/0|1=1/0|0=0
// 1^1=0/1^0=1/0^1=1/0^0=0
private char[] arr;
// 设dp[s][e][r]为从索引s到索引e值为r的方案数。
private int[][][] dp;
private int getBoolAns(int val1, int val2, char operator) {
switch (operator) {
case '&':
return val1 & val2;
case '|':
return val1 | val2;
case '^':
return val1 ^ val2;
}
return val1 & val2;
}
/**
* 返回从索引start到end值为result的不同括号方案的个数
*/
private int rec(int start, int end, int result) {
if (start == end) {
return arr[start] - '0' == result ? 1 : 0;
}
if (dp[start][end][result] != -1) {
return dp[start][end][result];
}
int ansCount = 0;
for (int k = start; k < end; k+=2) {
char operator = arr[k + 1];
for (int i = 0; i <= 1; i++) {
for (int j = 0; j <= 1; j++) {
if (getBoolAns(i, j, operator) == result) {
ansCount += rec(start, k, i) * rec(k + 2, end, j);
}
}
}
}
dp[start][end][result] = ansCount;
return ansCount;
}
public int countEval(String s, int result) {
arr = s.toCharArray();
int len = arr.length;
dp = new int[len][len][2];
for (int i = 0; i < len; i++) {
for (int j = 0; j < len; j++) {
Arrays.fill(dp[i][j], -1);
}
}
return rec(0, len - 1, result);
}
}
统计不同回文子序列
class Solution {
public int countPalindromicSubsequences(String S) {
int n = S.length();
int[][] dp = new int[n][n]; // dp[i][j]表示[i,j]下标范围内的回文子序列数量
char[] ch = S.toCharArray();
for (int i = 0; i < n; i++) {
dp[i][i] = 1;
}
for (int len = 2; len <= n; len++) {//长度从2开始
for (int i = 0; i < n - len + 1; i++) {
int j = i + len - 1;
if (ch[i] != ch[j]) {
dp[i][j] = dp[i + 1][j] + dp[i][j - 1] - dp[i + 1][j - 1]; // 两个子区间的dp值减去重复计算后的dp值
} else {
dp[i][j] = dp[i + 1][j - 1] * 2; //两端重复数相当于子串的回文数 * 2
/*
例: b......b 中......的子序列为{x}
那么 b + {x} + b 也是回文串 所以乘2
*/
//去重及增加回文串
int l = i + 1, r = j - 1;
while (l <= r && ch[l] != ch[i]) l += 1;
while (l <= r && ch[r] != ch[i]) r -= 1;
if (l > r) dp[i][j] += 2;
/* 例"b.....b"
因为l 和 r 只有遇到端点值才会停下 如果l > r 说明 子区间中无端点值
当 除端点外的子区间[.....] 中没有端点值时 增加b 和 bb两种回文序列
*/
else if (l == r) dp[i][j] += 1;
/* 例:"b[..b..]b"
因为l 和 r 只有遇到端点值才会停下 如果l = r
证明除端点外的子区间中[..b..] 仅含有一个端点值且在最中间(如果含有两个及以上,l和r必定停在不同位置)
因为单个的端点值b已经出现过,无法增加。所以只能增加bb,因此 + 1
*/
else dp[i][j] -= dp[l + 1][r - 1];
/*
例b1..b2[...]b2..b1 因为l 和 r 只有遇到端点才会停下
如果l < r 则当 除端点之外的子区间中..b[...]b.. 中至少含有两个端点值
此时考虑子区间[...]的回文子序列为{x}, 则b1 + {x} + b1 和b2 + {x} + b2组成的子序列其实是一样的
我们在乘算的时候就多考虑了这一部分序列 所以要减去[...]的子序列数
且b 和 bb 都在子序列b2[...]b2中出现过了 也就没必要加上去
*/
}
dp[i][j] = dp[i][j] < 0 ? dp[i][j] + 1000000007 : dp[i][j] % 1000000007;
}
}
return dp[0][n - 1];
}
}
戳气球
// 每戳破一个气球 nums[i],得到的分数和该气球相邻的气球 nums[i-1] 和 nums[i+1] 是有相关性的,但子问题必须独立!
// 如果「正向思考」,就只能写出回溯算法;我们需要「反向思考」,想一想气球 i 和气球 j 之间最后一个被戳破的气球可能是哪一个?
class Solution {
public int maxCoins(int[] nums) {
int n = nums.length;
// 添加两侧的虚拟气球
int[] points = new int[n + 2];
points[0] = points[n + 1] = 1;
System.arraycopy(nums, 0, points, 1, n);
// dp[i][j]表示(i,j)的气球全被戳破可以获得的最高分数
int[][] dp = new int[n + 2][n + 2];
// 开始状态转移
// i 应该从下往上
for (int i = n; i >= 0; i--) {
// j 应该从左往右
for (int j = i + 1; j < n + 2; j++) {
// 最后戳破的气球是哪个?
for (int k = i + 1; k < j; k++) {
// 择优做选择
dp[i][j] = Math.max(
dp[i][j],
dp[i][k] + dp[k][j] + points[i] *points[j] *points[k]
);
}
}
}
return dp[0][n + 1];
}
}
多边形三角剖分的最低得分
public int minScoreTriangulation(int[] A) {
int len = A.length;
// dp[i][j]表示以(i,j)为底边,顶点在顺时针[i,j]区间时,将多边形划为三部分(可以为0),获得的最低分数
int[][] dp = new int[len][len];
for(int i = len - 3; i >= 0; i--){
// 至少有顶点可遍历才能构成三角形
for(int j = i + 2; j < len; j++){
// 遍历顶点
for(int m = i + 1; m < j; m++){
if(dp[i][j] == 0){
dp[i][j] = A[i] * A[m] * A[j] + dp[i][m] + dp[m][j];
}
else{
dp[i][j] = Math.min(dp[i][j],A[i] * A[j] * A[m] + dp[i][m] + dp[m][j]);
}
}
}
}
return dp[0][n - 1];
}
背包动态规划
- 0/1背包问题:有 n 种物品,物品 j 的体积为vj ,价值为wi 每种物品只有 1 个,只有选或者不选,如何使背包内物品体积总和小于等于背包容量V且价值最大。
// 普通
/*
dp[i][j] := 当前正在考虑第i个物品,已经考虑了 [0..i-1] 前 i 个物品,占用了 j 空间,所能取得的最大价值。
dp[i][j] = dp[i - 1][j] (当前物品不选,则前 i-1个物品占了j空间)
= dp[i - 1][j - v[i]] + w[i] (当前物品选,前i-1个物品只能占j-v[i] 空间)
*/
// 如果要求背包必须放满
/*
1. 初始化:初始时除了dp[0][0]=0(即没有物品且背包占用空间为0时价值为0)合法,其他所有都要初始化为-1,表示方案不合法。
2. 状态转移:dp[i-1][j-v[i]] + w[i]要更新进dp[i][j] 前,先要判断dp[i-1][j-v[i]]是否为-1,不为 -1,则 dp[i-1][j-v[i]]代表的物品组才能放出来。
*/
// 如果j从大向小推只需要一行空间
// dp[j] = max(dp[j], dp[j - v[i]] + w[i]) // j 从大往小推
// 状态表示与0/1背包问题相同
/*
dp[i][j] := 已经考虑了 [0..i-1] 前 i 个物品,占用了 j 空间,所能取得的最大价值。
dp[i][j] = dp[i - 1][j] (当前物品不选,则前 i-1个物品占了j空间)
= dp[i][j - v[i]] + w[i] (当前物品选,前i个物品只能占j - v[i]空间)
*/
// 如果j从小向大推只需要一行空间
// dp[j] = max(dp[j], dp[j - v[i]] + w[i]) // j 从小往大推
- 多重背包问题:每种物品有ci个。LeetCode没有多重背包问题。
- 背包的问题常见的有三种,第一个是求最值,这是背包的原始问题,第二个是体积要取到背包容量的最值,第三个是求方案数,即组合问题。如果是组合问题,即求方案数,是否需要考虑元素之间的顺序。需要考虑顺序有顺序的解法,不需要考虑顺序又有对应的解法,需要注意。

最后一块石头的重量II
class Solution {
// 把石头划分为两种,一种是需要石头来粉碎的,另一种是填充前一种需要的
// 当两种的重量均为总重量的一半时,全部粉碎光,求解用于填充的石头,容量上限是总重量一半,为0/1背包问题
public int lastStoneWeightII(int[] stones) {
// 数组总和
int sum = Arrays.stream(stones).sum();
// 背包容量
int volume = sum / 2;
// dp[j]表示背包容量为j时,能取到的最大体积
int[] dp = new int[volume + 1];
for(int i = 0; i < stones.length; i++){
for(int j = volume; j >= 0; j--){
if(j - stones[i] >= 0){
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
}
return sum - dp[volume] * 2;
}
}
组合总和 IV
class Solution {
// 完全背包问题,背包容量target,要求背包装满,求组合数,顺序不同有影响
public int combinationSum4(int[] nums, int target) {
int n = nums.length;
if(n == 0 || target <= 0){
return 0;
}
// dp[i]表示背包容量为i时的排列数有多少个(先遍历j再遍历i考虑的是组合数)
int[] dp = new int[target + 1];
dp[0] = 1;
for(int i = 1; i <= target; i++){
// dp[i] = sum(dp[i-nums[j]])即用j遍历nums,以nums[j]结尾的排列数之和(一个序列总有结尾)
for(int j = 0; j < n; j++){
if(i - nums[j] >= 0){
dp[i] += dp[i - nums[j]];
}
}
}
return dp[target];
}
}
目标和
class Solution {
/*
把所有符号为正的数总和设为一个背包的容量x;把所有符号为负的数总和设为一个背包的容量y。
令sum为数组总和,则x+y=sum,且x-y=S,有x=(S+sum)/2。
即,01背包问题,背包容量为x,要求背包恰好装满,求与顺序无关的组合数。
*/
public int findTargetSumWays(int[] nums, int S) {
int sum = Arrays.stream(nums).sum();
// x必须是整数,且目标和不可能大于总和。
if ((sum + S) % 2 == 1 || S > sum){
return 0;
}
int n = nums.length;
int volume = (S + sum) / 2;
// dp[j]表示容量为j时的组合数
int[] dp = new int[volume + 1];
dp[0] = 1;
for(int i = 0; i < n; i++){
for(int j = volume; j >= nums[i]; j--){
dp[j] += dp[j - nums[i]];
}
}
return dp[volume];
}
}
状态压缩
- 状态压缩动态规划,是利用计算机 二进制 的性质来描述状态的一种动态规划方式。
- 状压其实是一种很暴力的算法,因为他需要遍历每个状态,所以将会出现 2n个状态数量,n一般需要小于等于20才可以考虑。
- 用位运算可以表示集合的常见操作:
- c 插入 A :A |= (1 << c)
- A 删除 c :A &= ~(1 << c)
- A 置空 :A = 0
- 并集 :A | B
- 交集 :A & B
- 全集 :(1 << n) - 1
- 补集 :((1 << n) - 1) ^ A
- 子集 :(A & B) == B
- 判断是否是 2 的幂 :A & (A - 1) == 0 (2的幂第一位为1其余位为0)
- 最低位的 1 变为 0 :n &= (n - 1) (二进制 xxxx10000-1 = xxxx01111)
- 最低位的 1:A & (-A),最低位的 1 一般记为 lowbit(A),表示 A 的二进制表达式中最低位的 1 所对应的值。(补码最低位的1及其右边的0不变,左边的位全部取反)
- 最高位的1:
// p为最低位的1,依次把集合中所有最低位的1全都清掉
int p = lowbit(A)
while(p != A)
{
A -= p;
p = lowbit(A);
}
return p;
- 枚举A的子集:
for(subset = (A - 1) & A; subset != A; subset = (subset - 1) & A)
{
...
}
- 枚举全集的子集:
for(i = 0; i <= (1 << n) - 1; ++i)
{
...
}
我能赢吗
class Solution {
public boolean canIWin(int maxChoosableInteger, int desiredTotal) {
// 特判,如果总的点数和不能达到desiredTotal,判输
if((1+maxChoosableInteger)*maxChoosableInteger/2 < desiredTotal)
return false;
// 使用dp数组来记录对应状态下先手是否能赢的情况
return helper(maxChoosableInteger, desiredTotal, new Boolean[1 << maxChoosableInteger], 0);
}
public boolean helper(int maxChoosableInteger, int desiredTotal, Boolean[] dp, int state){
if(dp[state] != null)
return dp[state];
for(int i = 1; i <= maxChoosableInteger; i++){
// 选择i其实就是把state对应二进制从左往右数第i个位置的位置为1
int cur = 1 << (i - 1);
// 表示数字i被使用过了
if((cur & state) != 0)
continue;
// 如果当前选择使得累积和大于等于desiredTotal
// 又或者当前选择之后,另一个人的选择必输,说明当前必赢
if(desiredTotal - i <= 0 ||
helper(maxChoosableInteger, desiredTotal - i, dp, state | cur) == false){
return dp[state] = true;
}
}
// 无论怎么选都无法让对手输,那么就是自己输了
return dp[state] = false;
}
}
计数问题
- 一般有两种做法:
- 找到组合数公式,然后用 DP 的方式或者用含阶乘的公式求组合数
- 找到递归关系,然后以 DP 的方式求这个递推关系,如果是线性递推关系,可以用矩阵快速幂加速
- 很多问题用动态规划的思考方式思考时,可能会发现状态不是很好设计,或者不是很好转移,组合数公式也不好想,此时需要手算一些例子,看看能不能找到一些规律,找到突破口进而得到递推公式。
- 卡特兰数:满足递推式f(n)=f(0)∗f(n−1)+f(1)∗f(n−2)+...+f(n−1)∗f(0)
- 通项:f(n)=n+1C2nn
- 通项变形:f(n)=C2nn−C2nn−1
- 递推式:f(n)=∑i=0n−1f(i)×f(n−i−1)
- 卢卡斯定理:用于求组合数对某质数的模。
- 杨辉三角:组合数公式Cmn=n!(m−n)!m!直接计算时,m=21时就已经溢出,可以使用递推式Cmn=Cm−1n−1+Cm−1n计算,但当所需要计算的值本身就溢出时,往往要求返回对其取模的结果。
- 快速幂法:根据费马小定理有若p为质数,a为正整数,且a、p互质则ap−1≡1(modp),即ap−2为a在modp下的逆元,使用快速幂求解。此时
Cmn=m!×inv(n!)×inv((m−n)!)(modp),mod p的阶乘和逆元可预处理出来。(要求p>m)
final static int MOD = 1000000007;
// C_{m}^{n}组合数快速幂取模 m>=n, m>0
private static long combmod(long m, long n){
if(n > m){
return 0;
}
long up = 1, down = 1;// 分子分母
for(long i = m - n + 1; i <= m; i++){
up = up * i % MOD;
}
for(long i = 1; i <= n; i++){
down = down * i % MOD;
}
return up * inv(down, MOD) % MOD;
}
// 快速幂(取模):n为底数,m为指数,复杂度O(logm)
private static long quickpow(long n, long m) {
long res = 1;
long base = n % MOD;
while(m != 0) {
// 判断m的二进制最后一位是否为1
if ((m&1) == 1) {
res = res * base % MOD;
}
base = base * base % MOD;
// 将m的二进制的最后一位移除
m = m >> 1;
}
return res;
}
// 求a关于p逆元,p为素数
private static long inv(long a, long p){
return quickpow(a, p-2);
}
- 卢卡斯(lucas)定理:快速幂法如果p比m小,不能保证逆元存在。公式为$C(m,n)%p=C(m/p,n/p)*C(m%p,n%p)%p$
private static long lucas(long m, long n){
if(n == 0){
return 1;
}
return combmod(m % MOD, n % MOD) * lucas(m / MOD, n / MOD) % MOD;
}
- 矩阵快速幂(方阵):与快速幂思路相同,但做的是矩阵乘法。
class Matrix{
int[][] matrix;
int len;
// 生成空矩阵
Matrix(int n){
len = n;
matrix = new int[n][n];
}
// 由数组生成矩阵
Matrix(int[][] m){
len = m.length;
matrix = new int[len][len];
for(int i = 0; i < len; i++){
matrix[i] = Arrays.copyOf(m[i], m.length);
}
}
// 矩阵乘法(方阵)
public static Matrix multiple(Matrix a, Matrix b){
Matrix res = new Matrix(a.len);
for(int i = 0; i < a.len; ++i){
for(int j = 0; j < a.len; ++j){
for(int k = 0; k < a.len; ++k){
res.matrix[i][j] += a.matrix[i][k] * b.matrix[k][j];
}
}
}
return res;
}
// 矩阵快速幂(方阵)
public static Matrix power(Matrix a, int n){
Matrix res = new Matrix(a.len);
for(int i = 0; i < a.len; ++i){
res.matrix[i][i] = 1;
}
Matrix base = new Matrix(a.matrix);
while(n != 0){
if((n&1) == 1){
res = Matrix.multiple(res, base);
}
base = Matrix.multiple(base, base);
n = n >> 1;
}
return res;
}
@Override
public String toString(){
StringBuilder sb = new StringBuilder();
for(int i = 0; i < len; i++){
sb.append("[");
for(int j = 0; j < len; j++){
sb.append(matrix[i][j] + " ");
}
sb.append("]\n");
}
return sb.toString();
}
}
数位动态规划
- 解决的问题:
- 满足某些条件的数字个数
- 将x∈[L,R]代到一个函数 f(x) 中,一个数字 x 的 f(x) 值为一次贡献的量,求总的贡献
- 思路:将范围按位划分来考虑。
- 当高位未顶到上界(可能是未被限制,也可能是被限制了但是选的数未顶到上界),则低位的数字无限制
- 当高位顶到了上界,则低位的数字 被限制 且要分类:顶到上界和未顶到上界
- 状态设计和状态转移:
dp[pos][lim] ,pos 为当前的数位 N-1 ~ 0 ,lim 表示是否顶到上界,对于 -1 的地方,pos 到 -1 的时候可以 return 1,使得个位的枚举有效。
// 不带前导零状态的数位 dp 模板
// pos:当前的数位(最高位->最低位)
// lim:0为前一位达到上界,1为前一位未达到上界(当前位无约束)
// digits[i]表示第 i 位的上界
// num_set:可选数字集合
private int getdp(int pos, int lim, int[] digits, int[] num_set, int[][] dp){
// 使得个位的枚举有效
if(pos == -1){
return 1;
}
// 返回已经计算出来的结果
if(dp[pos][lim] != -1){
return dp[pos][lim];
}
dp[pos][lim] = 0;
int up = lim == 1 ? digits[pos] : 9; // 当前要枚举到的上界
for(int i: num_set){ // 枚举当前位所有可能数字
if(i > up)
break;
dp[pos][lim] += getdp(pos - 1, (lim == 1 && i == up) ? 0 : 1, digits, num_set, dp); // 本位被限制且选顶到上界的数字,下一位才被限制
}
return dp[pos][lim];
}
- 前导零的分析:增加 zero 状态, 表示高位是否是前导零。
1. 如果高位选了前导零,则当前位无限制,且还可以选前导零。
2. 如果高位没有选前导零且未顶到上界,则当前位在可选数字集合的范围内无限制。
3. 如果高位顶到了上界,则当前位的选择被限制。
中心对称数III
class Solution {
// 分别计算以low和high为上限满足要求的数字,相减得到区间部分。
// 位数少于上限数字位数的数字可以直接用排列组合计算,位数等于上限数字位数的数字需要利用数位DP进行计算。
int[] candidate1 = {0, 1, 6, 8, 9};
int[] candidate2 = {0, 1, 8};
public int strobogrammaticInRange(String low, String high) {
if(Long.valueOf(low) > Long.valueOf(high)){
return 0;
}
if(low.charAt(0) == '0'){
return getCount(high);
}
else{
low = String.valueOf(Long.valueOf(low) - 1);
return getCount(high) - getCount(low);
}
}
// 快速幂:n为底数,m为指数,复杂度O(logm)
private long quickpow(long n, long m) {
long res = 1;
long base = n;
while(m != 0) {
// 判断m的二进制最后一位是否为1
if ((m & 1) == 1) {
res = res * base;
}
base = base * base;
// 将m的二进制的最后一位移除
m = m >> 1;
}
return res;
}
private int getCount(String str){
long res = 0;
// 位数少于上限数字位数的数字,使用排列组合计算
// 用i遍历当前位数
for(int i = 1; i < str.length(); i++){
// 实际可以选择的位数个数
int exp = i / 2;
// 位数是偶数,第一位有四种选法,其他位有五种选法
if(i % 2 == 0){
res += 4 * quickpow(5, exp - 1);
}
// 位数是奇数,第一位有4种选法,中间位3种选法,其他位有5种选法
else{
// 第一位就是中间位
if(i == 1){
res += 3;
}
else{
res += 4 * 3 * quickpow(5, exp - 1);
}
}
}
// 位数等于上限数字位数的数字,使用数位动态规划计算
// dp[i][0/1]表示选择的第i位是上界/不是上界时前i位的选法总数
int[][] dp = new int[str.length() / 2 + 1][2];
// 初始化
dp[0][0] = 1;
for(int i = 1; i <= str.length() / 2; i++){
// 获取第i位数的上界(高位->低位)
int num = str.charAt(i-1) - '0';
// 为第i位数选择数,第一位不能为0,计算不是上界满足要求的选法
for(int j = (i == 1 ? 1 : 0); j < 5; j++){
// 更高位不是上界,那么当前位随便选。
dp[i][1] += dp[i-1][1];
}
int j;
for(j = (i == 1 ? 1 : 0); j < 5 && candidate1[j] < num; j++){
// 更高位是上界,当前位不是上界
dp[i][1] += dp[i-1][0];
}
// 更高位是上界,当前位也是上界
if(candidate1[j] == num){
dp[i][0] += dp[i-1][0];
}
}
// 分奇数长度和偶数长度进行计算
// 上界长度为奇数
if(str.length() % 2 == 1){
// 正中间的上限
int num = str.charAt(str.length() / 2) - '0';
// 正中间的数只有3种选择
for(int i = 0; i < 3; i++){
res += dp[str.length() / 2][1];
}
int i;
for(i = 0; i < 3 && candidate2[i] < num; i++){
res += dp[str.length() / 2][0];
}
// 验证数字翻转后是否在范围内
if(i != 3 && candidate2[i] == num && dp[str.length() / 2][0] != 0 && isValid(str)){
res += dp[str.length() / 2][0];
}
}
// 上界长度为偶数
else{
res += dp[str.length() / 2][1];
// 验证数字翻转后是否在范围内
if(dp[str.length() / 2][0] != 0 && isValid(str)){
res += dp[str.length() / 2][0];
}
}
return (int) res;
}
// 验证str表示的数旋转180度后还是否小于上界
private boolean isValid(String str){
if(str.length() == 1){
return true;
}
StringBuilder sb = new StringBuilder();
sb.append(str.substring(0, (str.length() + 1) / 2));
for(int i = str.length() / 2 - 1; i >= 0; i--){
if(str.charAt(i) == '6'){
sb.append("9");
}
else if(str.charAt(i) == '9'){
sb.append("6");
}
else{
sb.append(str.charAt(i));
}
}
return Long.valueOf(sb.toString()) <= Long.valueOf(str) ? true : false;
}
}
至少有1位重复的数字
class Solution {
public int numDupDigitsAtMostN(int N) {
if(N <= 10){
return 0;
}
char[] ntop = String.valueOf(N).toCharArray();
int sum = 0;
// 分为两个部分,位数小于N的和位数等于N的
// 位数小于N的部分直接用数学公式计算
// 位数等于N的部分用数位DP计算
int[][] dp = new int[ntop.length][2];
// visited标记i位数字是否已经被选过
boolean[] visited = new boolean[10];
sum = N - getdp(0, 1, ntop, visited, dp) - countNumbersWithUniqueDigits(ntop.length - 1) + 1;
return sum;
}
// lim为1时表示前一位达到上界,当前位被限制
private int getdp(int index, int lim, char[] ntop, boolean[] visited, int[][] dp){
// 使得个位的枚举有效
if(index == ntop.length){
return 1;
}
// 返回已经计算出来的结果
if(dp[index][lim] != 0){
return dp[index][lim];
}
dp[index][lim] = 0;
// 当前要枚举到的上界
int up = (lim == 1 ? ntop[index] - '0' : 9);
// 枚举当前位所有可能数字
for(int i = (index == 0 ? 1 : 0); i < 10; i++){
if(i > up){
break;
}
if(visited[i]){
continue;
}
visited[i] = true;
dp[index][lim] += getdp(index + 1, (lim == 1 && i == up) ? 1 : 0, ntop, visited, dp);
visited[i] = false;
}
return dp[index][lim];
}
public int countNumbersWithUniqueDigits(int n) {
// 保存0-10的阶乘
int[] fac = new int[11];
fac[0] = 1;
for(int i = 1; i < 11; i++){
fac[i] = i * fac[i - 1];
}
//
int sum = 0;
for(int i = 0 ; i < n; i++){
sum += calculateA(fac, 10, i + 1);
if(i != 0){
sum -= calculateA(fac, 9, i);
}
}
return sum;
}
// 计算排列数Amn
private int calculateA(int[] fac, int m, int n){
return fac[m] / fac[m-n];
}
// 快速幂
private long quickpow(long n, long m) {
long res = 1;
long base = n;
while(m != 0) {
// 判断m的二进制最后一位是否为1
if ((m & 1) == 1) {
res = res * base;
}
base = base * base;
// 将m的二进制的最后一位移除
m = m >> 1;
}
return res;
}
}
区间调度问题
- 给你很多形如
[start, end]的闭区间,请你设计一个算法,算出这些区间中最多有几个互不相交的区间。
- 贪心解法:
- 从区间集合 intvs 中选择一个区间 x,这个 x 是在当前所有区间中结束最早的(end 最小)。可以按每个区间的 end 数值升序排序
- 把所有与 x 区间相交的区间从区间集合 intvs 中删除。(如果一个区间不想与 x 的 end 相交,它的 start 必须要大于(或等于)x 的 end)
- 重复步骤 1 和 2,直到 intvs 为空为止。之前选出的那些 x 就是最大不相交子集。
public int intervalSchedule(int[][] intvs) {
if (intvs.length == 0) return 0;
// 按 end 升序排序
Arrays.sort(intvs, (a, b) -> a[1] - b[1]);
// 至少有一个区间不相交
int count = 1;
// 排序后,第一个区间就是 x
int x_end = intvs[0][1];
for (int[] interval : intvs) {
int start = interval[0];
if (start >= x_end) {
// 找到下一个选择的区间了
count++;
x_end = interval[1];
}
}
return count;
}



